归并排序,先拆后合
动画演示:
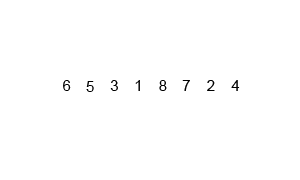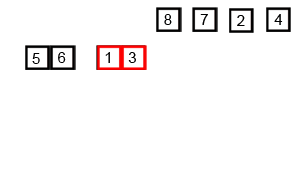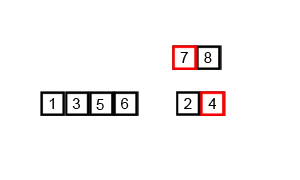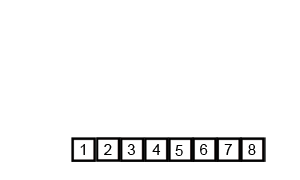
要对其“先拆后合”,理应通过下标值进行,
假设有个长度为10的数组,则下标为 0123456789,
拆的过程:
0123456789
01234 56789
012 34 567 89
01 2 3 4 56 7 8 9
0 1 5 6
并不难发现,这个过程其实是一棵二叉树:
0123456789
_____________/ \_____________
/ \
01234 56789
_____/ \_____ _____/ \_____
/ \ / \
012 34 567 89
_/ \_ _/ \_ _/ \_ _/ \_
/ \ / \ / \ / \
01 2 3 4 56 7 8 9
/ \ / \
0 1 5 6
合并的过程:
自下而上合并,
如将[0], [1] 合并为同时包含这两个数的序列, 对比大小调整其顺序
另如将[0, 1, 2], [3, 4] 合并,此时这两个子序列已有序,要将其合并需要:
1、定义一个临时列表 temp_datas
2、定义两个游走下标,i, j,初始值分别为两个子序列的第一个值, 由于两个子序列都已经有序,
因此,只需要依次把更小的那个放到临时列表中,最后再拷贝回原列表就可以了
是否可通过遍历二叉树的方式,来进行此算法,答案是可以的。
1、拆分:可以通过对半拆分找到左右孩子
2、合并:需要自下而上且先把左右孩子变成有序,这和后序遍历是一样的
递归方式实现:
def merge_sort_recursion4(datas):
def _divide(start_index, end_index):
if start_index == end_index:
return
mid = (start_index + end_index) // 2
_divide(start_index, mid)
_divide(mid + 1, end_index)
temp_i, i, j = start_index, start_index, mid + 1
while i <= mid and j <= end_index:
if datas[i] <= datas[j]:
temp_datas[temp_i] = datas[i]
i += 1
else:
temp_datas[temp_i] = datas[j]
j += 1
temp_i += 1
while i <= mid:
temp_datas[temp_i] = datas[i]
i += 1
temp_i += 1
while j <= end_index:
temp_datas[temp_i] = datas[j]
j += 1
temp_i += 1
for i in range(start_index, end_index + 1):
datas[i] = temp_datas[i]
temp_datas = [0] * len(datas)
_divide(0, len(datas) - 1)
return datas
非递归方式实现一:
利用栈,先把每趟拆分过程全部记录下来,然后依次从栈中每趟的拆分结果取出,进行合并,
这种方式将拆分与合并进行分离,加强了代码的可读性
def merge_sort_iteration6(datas):
length = len(datas)
mid = (length - 1) // 2
op_stack = [[(0, mid), (mid+1, length - 1)], ]
while True:
divides = op_stack[-1]
new_divides = []
for d in divides:
if d[0] == d[1]:
continue
mid = (d[0] + d[1]) // 2
new_divides.append((d[0], mid))
new_divides.append((mid+1, d[1]))
if not new_divides:
break
op_stack.append(new_divides)
temp_datas = [0] * length
while op_stack:
divides = op_stack.pop()
for k in range(0, len(divides), 2):
i, mid = divides[k]
j, end = divides[k+1]
temp_i = i
while i <= mid and j <= end:
if datas[i] <= datas[j]:
temp_datas[temp_i] = datas[i]
i += 1
else:
temp_datas[temp_i] = datas[j]
j += 1
temp_i += 1
while i <= mid:
temp_datas[temp_i] = datas[i]
i += 1
temp_i += 1
while j <= end:
temp_datas[temp_i] = datas[j]
j += 1
temp_i += 1
for i in range(divides[k][0], end+1):
datas[i] = temp_datas[i]
return datas
非递归方式实现二:
这种方式不是把拆分过程看作是二叉树,而是偏数学的一个方式:
一开始是 2个 2个为一组进行合并处理,而后是 4个 4个为一组:
从2开始等比增长
一、step = 2
01 23 45 67 89
二、step = 4
0123 4567 89
三、step = 8
01234567 89
二中出现了89这样长度小于step的序列,这种的只要将其与前一个序列4567进行合并就行了
def merge_sort_math6(datas):
def _merge(start, mid, j, end):
i = temp_i = start
while i <= mid and j <= end:
if datas[i] <= datas[j]:
temp_datas[temp_i] = datas[i]
i += 1
else:
temp_datas[temp_i] = datas[j]
j += 1
temp_i += 1
while i <= mid:
temp_datas[temp_i] = datas[i]
i += 1
temp_i += 1
while j <= end:
temp_datas[temp_i] = datas[j]
j += 1
temp_i += 1
for i in range(start, end+1):
datas[i] = temp_datas[i]
length = len(datas)
temp_datas = [0] * length
step = 2
while step <= length:
i = 0
while i + step - 1 < length:
end = i + step - 1
mid = (i + end) // 2
_merge(i, mid, mid+1, end)
i += step
if i < length:
_merge(i - step, i-1, i, length - 1)
step *= 2
return datas
