圆圈中最后剩下的数字
0,1,n-1这n个数字排成一个圆圈,从数字0开始,每次从这个圆圈里删除第m个数字。求出这个圆圈里剩下的最后一个数字。
例如,0、1、2、3、4这5个数字组成一个圆圈,从数字0开始每次删除第3个数字,则删除的前4个数字依次是2、0、4、1,因此最后剩下的数字是3。
示例 1:
输入: n = 5, m = 3
输出: 3
示例 2:
输入: n = 10, m = 17
输出: 2
限制:
1 <= n <= 10^5
1 <= m <= 10^6
自我解答:
闹心,又是被虐的一次。。。初看这个题觉得很简单,感觉自己10分钟之内就能写出来。
用程序模拟很容易实现,但若数比较大,应该会超时,试着写出来了,果然。但实在想不到其他的办法了。
网友解答:
数学,数学,又是数学。这是一个经典数学问题-- “约瑟夫环”:
有 N 个人 围成一圈,从第一个人开始报数,每 M 个人便杀掉一人,请问最后留下的是第几个人。
公式:
f(N, M) = (f(N−1, M) + M) % N
· f(N, M)表示,N个人报数,每报到M时杀掉那个人,最终胜利者的编号
· f(N−1, M)表示,N-1个人报数,每报到M时杀掉那个人,最终胜利者的编号
公式推导:
我们用数字表示每一个人:1、2、3、4、5、6、7、8、9、10、11
11个人,他们先排成一排,假设每报到3的人被杀掉。
图示:
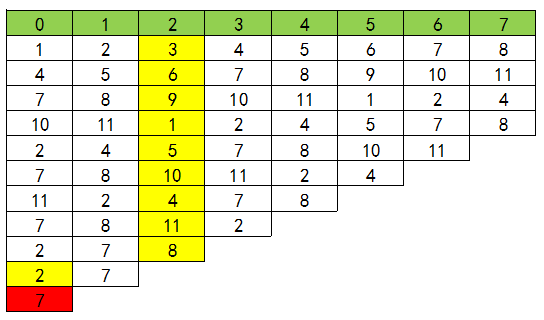
将上面表格的每一行看成数组,这个公式描述的是:幸存者在这一轮的下标位置
f(1, 3):只有1个人了,那个人就是获胜者,他的下标位置是0
f(2, 3) = (f(1, 3) + 3) % 2 = 3 % 2 = 1:在有2个人的时候,胜利者的下标位置为1
f(3, 3) = (f(2, 3) + 3) % 3 = 4 % 3 = 1:在有3个人的时候,胜利者的下标位置为1
f(4, 3) = (f(3, 3) + 3) % 4 = 4 % 4 = 0:在有4个人的时候,胜利者的下标位置为0
……
f(11 , 3) = 6
算法实现:
def last_remaining(n: int, m: int) -> int:
left = 0
for i in range(2, n + 1):
left = (left + m) % i
return left
if __name__ == '__main__':
print(last_remaining(5, 3))
约瑟夫环参考链接:https://blog.csdn.net/u011500062/article/details/72855826
原题链接:https://leetcode-cn.com/problems/yuan-quan-zhong-zui-hou-sheng-xia-de-shu-zi-lcof
